Il momento delle forze

Un corpo rigido, a differenza del punto materiale, può anche ruotare.

"Il braccio di una forza F rispetto a un punto O è dato dalla distanza tra il punto O e la retta che contiene F"
Definiamo quindi il momento di una forza  come "Il movimento di una forza F rispetto a un punto O è uguale al prodotto dell'intensità F della forza  per il braccio b".

M=F b           F=M/b         b=M/F               (ricorda  b=braccio)

Il momento della forza ha segno positivo se ruota in senso antiorario, negativo in senso orario.
L'unità di misura del momento  è  N m.

Il momento di una coppia di forze è data da due forze, uguali e opposte, applicate in due punti diversi di un corpo rigido.
"Definiamo il momento di una coppia  come la somma dei momenti delle forze rispetto al punto mediio O. Esso è uguale al prodotto dell'intensità F di una forza per la distanza d tra le rette di azione delle due forze"

M= F d
esempio: pensiamo alla chiave nella toppa della serratura, ad una bici quando ruotiamo il manubrio, la maniglia di una porta, ecc
quindi M=Fb + Fb   dove d= distanza  e  comprende i due bracci b1+b2
i segni sono come per il momento della forza visto sopra antiorario=positivo e orario=negativo

Il momento di una forza è una grandezza vettoriale avente la drezione perpendicolare al piano individuato da r  e  F e verso offerto dalla regola della mano destra allorquando r si sovrappone ad F descrivendo l'angolo alfa
possiamo scrivere cosi il prodotto verttoriale: M = r∧ F
ed in modulo: M = r F senϑ   dove senϑ è l'angolo che si forma tra due vettori; ed M è dato dalla regola della mano destra.

Effetto di più forze su un corpo rigido

Due o più forze applicate ad un punto materiale danno una forza risultante che è la somma delle forze applicate. Tutto questo è vero fino ad un certo punto, infatti constatato che
"una forza che agisce su un corpo rigido può essere spostata lungo la sua retta d'azione in un altro punto dello stesso  corpo, senza che l'effetto della forza cambi".
Possono verificarsi casi diversi tipo:
1) le forze sono applicate lungo la stessa retta d'azione;
2) le forze sono dette parallele (concordi e discordi);
3) le forze agiscono lungo rette d'azione che s'intersecano, in questo caso si dicono concorrenti.

caso 1 stessa retta d'azione    

 





caso 2 parallele concordi

caso 2 parallele discordi

 

caso 3 concorrenti (si applica la regola del parallelogramma)

Laboratorio:misure con il calibro e il righello

Una prova che non manca mai nel programma di laboratorio di fisica è la misura diretta con uno strumento di misura molto usato non solo in laboratorio ma anche nella vita quotidiana, a casa, sul lavoro, nell'officine ecc. Stiamo parlando del calibro a cursore, uno strumento molto preciso ed accurato.

Per la descrizione del calibro e del modello della prova di laboratorio vi rimando ai seguenti link:

 istruzioni uso calibro                   misura di un oggetto con il calibro

ps. le immagini de istruzioni uso calibro non si vedono bene pertanto vi rimando al seguente link:

uso del calibro                         ricerca sul calibro                                                  istruzioni

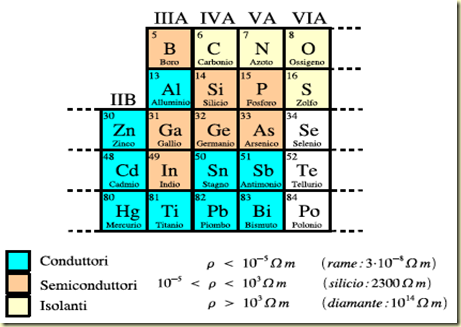
Conduttori, semiconduttori e isolanti

 

Le sostanze che favoriscono al loro interno il passaggio della corrente elettrica sono dette conduttori; quelle invece che impediscono il passaggio della corrente sono dette isolanti.
Solo poche sostanze, principalmente i metalli, sono buoni conduttori dell’elettricità. Ciò dipende dal fatto che i metalli sono composti da atomi che hanno una struttura elettronica costituita da una serie di livelli (bande) completamente occupati ed un livello più esterno non completamente occupato, contenente uno, due o a volte anche tre elettroni di valenza . Nei metalli allo stato solido, gli elettroni di valenza sono praticamente liberi di muoversi; essi si trovano in un livello di energia più elevato: si dice che sono in banda di conduzione.
Un campo elettrico applicato al metallo, anche se piccolo, produce un moto di deriva e quindi una corrente elettrica.
In molte sostanze tuttavia, gli elettroni di valenza sono legati agli ioni positivi del reticolo. A causa della mancanza di elettroni liberi e quindi di portatori di carica, in queste sostanze è molto difficile produrre una corrente elettrica ; queste sostanze sono chiamate dielettrici e sono isolanti.
Vi è un’altra categoria di sostanze, chiamate semiconduttori costituite da materiali che hanno un comportamento diverso sia dai conduttori che dagli isolanti. In essi gli elettroni riempiono tutta la banda di valenza e non vi sono elettroni “liberi” nella banda di conduzione, proprio come negli isolanti. Nei semiconduttori, però, l’energia necessaria per far passare un elettrone dalla banda di valenza a quella di conduzione è circa da 1/5 a 1/10 dell’energia di eccitazione di un isolante.
Un aumento di temperatura può avere l’effetto di liberare alcuni elettroni dai loro legami e mandarli in banda di conduzione. I semiconduttori hanno quindi una conducibilità elettrica.
I semiconduttori più usati sono germanio, silicio, tellurio.

tabella materiali conduttori

Materiale Resistività a 0 °C Coeff. di temperatura CONDUTTORI Argento Rame elettrolitico Rame Bronzo fosforoso Oro Alluminio Tungsteno Ottone Ferro puro Platino Ferro dolce Stagno Piombo Argentana Manganina Ferro-silicio Costantana Ferro-nichel Mercurio Nichel-cromo 0,015 0,016 0,017 0,018 0,021 0,028 0,050 0,085 0,100 0,103 0,13 0,13 0,20 0,35 0,40 0,50 0,50 0,80 0,94 1 0,0036 0,0042 0,0043 0,0040 0,0036 0,0043 0,0042 0,0039 0,0050 0,0036 0,0048 0,0045 0,0043 0,00017 0,00001 0,001 0,000008 0,0007 0,00089 0,0001 Il coefficiente di temperatura a0 viene fornito per una temperatura di riferimento di 0 °C. Qualora si abbia una temperatura di riferimento f °C, il nuovo valore di af si ricava dalla formula: af = a0 / 1 + a0 x f Tabella semiconduttori

Multipli e sottomultipli, unità fondamentali e derivate

Sistema Internazionale-prefissi fattore di moltiplicazione prefisso simbolo valore 10 24 yotta Y 1 000 000 000 000 000 000 000 000 10 21 zetta Z 1 000 000 000 000 000 000 000 10 18 exa E 1 000 000 000 000 000 000 10 15 peta P 1 000 000 000 000 000 10 12 tera T 1 000 000 000 000 10 9 giga G 1 000 000 000 10 6 mega M 1 000 000 10 3 chilo k 1 000 10 2 etto h 100 10 1 deca da 10 10 -1 deci d 0.1 10 -2 centi c 0.01 10 -3 milli m 0.001 10 -6 micro µ 0.000 001 10 -9 nano n 0.000 000 001 10 -12 pico p 0.000 000 000 001 10 -15 femto f 0.000 000 000 000 001 10 -18 atto a 0.000 000 000 000 000 001 10 -21 zepto z 0.000 000 000 000 000 000 001 10 -24 yocto y 0.000 000 000 000 000 000 000 001 Unità fondamentali

Grandezza fisica	Simbolo della grandezza	Nome dell'unità SI	Simbolo dell'unità SI
lunghezza	l	metro	m
massa	m	chilogrammo	kg
intervallo di tempo	t	secondo	s
Intensità di corrente	I, i	ampere	A
temperatura assoluta	T	kelvin	K
quantità di sostanza	n	mole	mol
intensità luminosa	Iv	candela	cd

Unità derivate

Grandezza fisica	Simbolo della grandezza	Nome dell'unità SI	Simbolo dell'unità SI	Equivalenza in termini di unità fondamentali SI
Nomi e simboli speciali
frequenza	f, ν	hertz	Hz	s−1
forza	F	newton	N	kg · m · s−2
pressione, sollecitazione, pressione di vapore	p	pascal	Pa	N · m−2	= kg · m−1 · s−2
energia, lavoro, calore	E, Q	joule	J	N · m	= kg · m2 · s−2
potenza, flusso radiante	P, W	watt	W	J · s−1	= kg · m2 · s−3
carica elettrica	q	coulomb	C	A · s
potenziale elettrico, forza elettromotrice, tensione elettrica	V, E	volt	V	J · C−1	= m2 · kg · s−3 · A−1
resistenza elettrica	R	ohm	Ω	V · A−1	= m2 · kg · s−3 · A−2
conduttanza elettrica	G	siemens	S	A · V−1	= s3 · A2 · m−2 · kg−1
capacità elettrica	C	farad	F	C · V−1	= s4 · A2 · m−2 · kg−1
densità flusso magnetico	B	tesla	T	V · s · m−2	= kg · s−2 · A−1
flusso magnetico	Φ(B)	weber	Wb	V · s	= m2 · kg · s−2 · A−1
induttanza	L	henry	H	V · s · A−1	= m2 · kg · s−2 · A−2
temperatura	T	grado Celsius	°C	K[2]
angolo piano[3]	φ, θ	radiante	rad	1	= m · m−1
angolo solido[3]	Ω	steradiante	sr	1	= m2 · m−2
flusso luminoso		lumen	lm	cd · sr
illuminamento		lux	lx	cd · sr · m−2
rifrazione	D	diottria	D	m−1
attività di un radionuclide [4]	A	becquerel	Bq	s−1
dose assorbita	D	gray	Gy	J · kg−1	= m2 · s−2
dose equivalente	H	sievert	Sv	J · kg−1	= m2 · s−2
dose efficace	E	sievert	Sv	J · kg−1	= m2 · s−2
attività catalitica		katal	kat	mol · s−1
Altre grandezze
area	A	metro quadro		m2
volume	V	metro cubo		m3
velocità	v	metro al secondo		m · s−1
velocità angolare	ω			s−1 rad · s−1
accelerazione	a			m · s−2
momento torcente				N · m	= m2 · kg · s−2
numero d'onda	n			m−1
densità	ρ			kg · m−3
volume specifico				m3 · kg−1
molarità SI[5]				mol · dm−3
volume molare	Vm			m3 · mol−1
capacità termica, entropia	C, S			J · K−1	= m2 · kg · s−2 · K−1
calore molare, entropia molare	Cm, Sm			J · K−1 · mol−1	= m2 · kg · s−2 · K−1 · mol−1
calore specifico, entropia specifica	c, s			J · K−1 · kg−1	= m2 · s−2 · K−1
energia molare	Em			J · mol−1	= m2 · kg · s−2 · mol−1
energia specifica	e			J · kg−1	= m2 · s−2
densità di energia	U			J · m−3	= m−1 · kg · s−2
tensione superficiale	σ			N · m−1	= J · m−2 = kg · s−2
densità di flusso calorico, irradianza	σ			W · m−2	= kg · s−3
conduttività termica				W · m−1 · K−1	= m · kg · s−3 · K−1
viscosità cinematica, coefficiente di diffusione	η			m2 · s−1
viscosità dinamica	ρ			N · s · m−2	= Pa · s = m−1 · kg · s−1
densità di carica elettrica				C · m−3	= m−3 · s · A
densità di corrente elettrica	j			A · m−2
conduttività elettrica	ρ			S · m−1	= m−3 · kg−1 · s3 · A2
conduttività molare	ρ			S · m2 · mol−1	= kg−1 · mol−1 · s3 · A2
permittività elettrica	ε			F · m−1	= m−3 · kg−1 · s4 · A2
permeabilità magnetica	μ			H · m−1	= m · kg · s−2 · A−2
(intensità) di campo elettrico	F, E			V · m−1	= m · kg · s−3 · A−1
(intensità) di campo magnetico	H			A · m−1
magnetizzazione	M			A · m−1
luminanza		[6]		cd · m−2
esposizione (raggi X e gamma)				C · kg−1	= kg−1 · s · A
tasso di dose assorbita				Gy · s−1	= m2 · s−3