giovedì 25 aprile 2013
mercoledì 3 aprile 2013
La spinta di Archimede
In questo post parliamo probalmente della più famosa legge, chi, non ha mai avuto a che fare, a scuola, con la spinta di Archimede!!
Esperienza di laboratorio: Spinta di Archimede
Archimede di Siracusa (in greco Ἀρχιμήδης; Siracusa, circa 287 a.C. – Siracusa, 212 a.C.) è stato un matematico, ingegnere, fisico e inventore greco antico (siceliota). È uno dei massimi scienziati della storia.
Perchè si dice spinta d'Archimede? Presto detto: se immergiamo un cilindro in un contenitore pieno di acqua, l'acqua esercita sul cilindro immerso una forza verso l'alto. Questa forza è uguale al peso dell'acqua sta dentro il volume del cilindro cavo. Pertanto la spinta di Archimede è quindi uguale al peso dell'acqua che il cilindro immergendosi, ha spostato.
Definizione: Un corpo immerso in un liquido subisce una forza diretta verso l'alto di intensità uguale al peso del liquido spostato.
Fa=g d V (N)
Fa= spinta di Archimede;
g= accelerazione di gravità (N/kg);
d= densità del corpo (liquido) (kg/m3);
V=volume del liquido spostato (m3).
Quando più grande è il volume del corpo immerso, tanto maggiore è la spinta verso l'alto, in quanto tanto maggiore è il volume di acqua spostato.
Il galleggiamento dei corpi: un corpo affonda, galleggia o sale quando la sua densità è rispettivamente maggiore uguale o minore di quella del liquido.
dimostrazione: Fa=Vdliquido g ma Fa è uguale Vdcorpo g
quindi possiamo scrivere Vdcorpo g = Vdliquido g
semplificando volume e costante g in ambi i termini otteniamo dcorpo=dliquido
per semplificazione sapendo che la costante g per la densità è uguale al peso specifico Ps ottenendo quindi Fa=Ps. V (N)
Esperienza di laboratorio: Spinta di Archimede
Archimede di Siracusa (in greco Ἀρχιμήδης; Siracusa, circa 287 a.C. – Siracusa, 212 a.C.) è stato un matematico, ingegnere, fisico e inventore greco antico (siceliota). È uno dei massimi scienziati della storia.
Perchè si dice spinta d'Archimede? Presto detto: se immergiamo un cilindro in un contenitore pieno di acqua, l'acqua esercita sul cilindro immerso una forza verso l'alto. Questa forza è uguale al peso dell'acqua sta dentro il volume del cilindro cavo. Pertanto la spinta di Archimede è quindi uguale al peso dell'acqua che il cilindro immergendosi, ha spostato.
Definizione: Un corpo immerso in un liquido subisce una forza diretta verso l'alto di intensità uguale al peso del liquido spostato.
Fa=g d V (N)
Fa= spinta di Archimede;
g= accelerazione di gravità (N/kg);
d= densità del corpo (liquido) (kg/m3);
V=volume del liquido spostato (m3).
Quando più grande è il volume del corpo immerso, tanto maggiore è la spinta verso l'alto, in quanto tanto maggiore è il volume di acqua spostato.
Il galleggiamento dei corpi: un corpo affonda, galleggia o sale quando la sua densità è rispettivamente maggiore uguale o minore di quella del liquido.
dimostrazione: Fa=Vdliquido g ma Fa è uguale Vdcorpo g
quindi possiamo scrivere Vdcorpo g = Vdliquido g
semplificando volume e costante g in ambi i termini otteniamo dcorpo=dliquido
per semplificazione sapendo che la costante g per la densità è uguale al peso specifico Ps ottenendo quindi Fa=Ps. V (N)
martedì 2 aprile 2013
La legge di Stevino
(Simone Stevino Bruges, 1548 – L'Aia, 1620 è stato un ingegnere, fisico e matematico fiammingo.)
La legge di Stevino afferma: la differenza di pressione all'interno di un liquido (pressione idrostatica) è direttamente proporzionale all'altezza della colonna di liquido tra le due sezioni considerate, dove il coefficiente di proporzionalità è il peso specifico Ps, definiamo il peso specifico come il peso dell'unità di volume, cioè: Peso specifico=peso/volume Ps=P/V; nel sistema internazionale l'unità di misura è il N/m3 .
La pressione idrostatica è quella che il liquido esercita sia sulle pareti e sulla base del recipiente che lo contiene. Cosa determina la pressione in un liquido? Possiamo dire che la quantità di liquido che fuoriesce sopra i fori più bassi nel caso di una bottiglia piena d'acqua a cui sono stati fatti dei piccoli fori è maggiore, quindi anche la pressione sarà maggiore e viceversa nei fori praticati in alto nella fattispecie alla bottiglia la pressione è minore.
Nell'esempio fatto sopra possiamo arrivare a dire che la forza peso esercita una pressione uguale in tutti posti alla stessa profondità.
Ritorniamo alla formula del peso specifico Ps=P/V dove P è la forza peso esercitata sul liquido e V è il volume, ma la forza peso P è uguale alla massa per l'accelerazione di gravità g pertanto possiamo scrivere Ps=( m g)/V ed anche che la densità d è uguale a massa m diviso il volume V, d=m/V per arrivare a Ps=d g (la densità per l'accelerazione di gravità)
Concludiamo dunque che la pressione dovuta al peso di un liquido è direttamente proporzionale sia alla densità del liquido sia alla profondità del liquido p=gdh dove:
p= la pressione esercitata da un liquido (Pa)
g= costante di proporzionalità (N/kg)
d= densità di un liquido (kg/m3)
h= profondità del liquido (m)
modello legge di Stevino
di quanto detto sopra abbiamo volutamente escludere la pressione atmosferica p0 quindi avremmo dovuto scrivere p= p0 + gdh
La legge di Stevino afferma: la differenza di pressione all'interno di un liquido (pressione idrostatica) è direttamente proporzionale all'altezza della colonna di liquido tra le due sezioni considerate, dove il coefficiente di proporzionalità è il peso specifico Ps, definiamo il peso specifico come il peso dell'unità di volume, cioè: Peso specifico=peso/volume Ps=P/V; nel sistema internazionale l'unità di misura è il N/m3 .
La pressione idrostatica è quella che il liquido esercita sia sulle pareti e sulla base del recipiente che lo contiene. Cosa determina la pressione in un liquido? Possiamo dire che la quantità di liquido che fuoriesce sopra i fori più bassi nel caso di una bottiglia piena d'acqua a cui sono stati fatti dei piccoli fori è maggiore, quindi anche la pressione sarà maggiore e viceversa nei fori praticati in alto nella fattispecie alla bottiglia la pressione è minore.
Nell'esempio fatto sopra possiamo arrivare a dire che la forza peso esercita una pressione uguale in tutti posti alla stessa profondità.
Ritorniamo alla formula del peso specifico Ps=P/V dove P è la forza peso esercitata sul liquido e V è il volume, ma la forza peso P è uguale alla massa per l'accelerazione di gravità g pertanto possiamo scrivere Ps=( m g)/V ed anche che la densità d è uguale a massa m diviso il volume V, d=m/V per arrivare a Ps=d g (la densità per l'accelerazione di gravità)
Concludiamo dunque che la pressione dovuta al peso di un liquido è direttamente proporzionale sia alla densità del liquido sia alla profondità del liquido p=gdh dove:
p= la pressione esercitata da un liquido (Pa)
g= costante di proporzionalità (N/kg)
d= densità di un liquido (kg/m3)
h= profondità del liquido (m)
modello legge di Stevino
La pressione
Ogni giorno nella nostra vita quotidiana ci troviamo a convivere con la forza peso del nostro corpo, forza che viene contro bilanciata da una forza uguale e contraria (reazione vincolare) al fine di restare in equilibrio. Ora facciamo un passo avanti e chiediamoci: cosa cambia in tutti quei corpi che applicandoci una forza subiscono delle deformazioni? La risposta sta nella dimensione della superficie di contatto tra ciò che applica la forza e ciò che la subisce, per fare degli esempi: scarpe-terreno, chiodo-legno, scarpe-neve, ecc.
Concludiamo dicendo che il diverso comportamento dei materiali sotto l'azione di una forza applicata è dovuto alla dimensione della superficie su cui è stata applicata tale forza.
La grandezza fisica è definita dal rapporto tra la forza F su cui agisce perpendicolarmente e la superficie S di contatto p=F/S (N/m2) (N/m2)=1 Pa (Pascal)
Definizione: possiamo dire dunque che la pressione di 1Pa è quella esercitata dalla forza di 1N che agisce perpendicolarmente su una superficie di 1m2 .
Legge di Pascal " la pressione esercitata su una superficie qualsiasi di un liquido si trasmette, con lo stesso valore, su ogni altra superficie a contatto con il liquido"
Quindi la pressione è una grandezza fisica scalare e derivata per definizione.
Data una superficie fissata, se la forza aumenta la pressione aumenta.
Data una forza fissata, se la superficie aumenta la pressione diminuisce.
_
Tuttavia, alla pressione viene associata una forza di pressione, indicata con P , diretta come la normale alla superficie, quindi pressione e forza hanno stesso verso e direzione.
ps. Ai fini operativi in Pascal non è una unità di misura molto utile e le si preferisce un suo multiplo il Bar: 1 Bar = 10000 Pa
Sono molte però le unità di misura che persistono nell'uso comune in vari campi della scienza
In meteorologia l'unità più usata è un sottomultiplo del Bar, il milliBar
1 mBar = 1 Bar/ 1000
In medicina la pressione sanguigna e quella dei fluidi in generale viene ancora misurata in milimmetri di mercurio (mmHg). Cioè si misura la pressione, del sangue ad esempio, confrontandola con quella che esercita una colonnina di mercurio, anche se i moderni apparecchi per misurare la pressione sono ormai elettronici, ben diversi dai vecchi sfigmomanometri.
1 mmHg = 133.322 Pa
In chimica si usa ancora fare gli esercizi considerando le atmosfere. L'atmosfera (Atm) è una grandezza correlata direttamente alla pressione che esercita l'involucro gassoso terrestre sulla terra. Una unità di misura storicamente ricavata durante i primi esperimenti sui gas perfetti.
1 Atm = 760 mmHg = 101325 Pa
Concludiamo dicendo che il diverso comportamento dei materiali sotto l'azione di una forza applicata è dovuto alla dimensione della superficie su cui è stata applicata tale forza.
La grandezza fisica è definita dal rapporto tra la forza F su cui agisce perpendicolarmente e la superficie S di contatto p=F/S (N/m2) (N/m2)=1 Pa (Pascal)
Blaise Pascal (Clermont-Ferrand, 19 giugno 1623 – Parigi, 19 agosto 1662) è stato un matematico, fisico, filosofo e teologo francese.
Contribuì a fondare la fluidodinamica. Inoltre fu tra i fondatori del calcolo delle probabilità e inventò la prima addizionatrice meccanica
Definizione: possiamo dire dunque che la pressione di 1Pa è quella esercitata dalla forza di 1N che agisce perpendicolarmente su una superficie di 1m2 .
Legge di Pascal " la pressione esercitata su una superficie qualsiasi di un liquido si trasmette, con lo stesso valore, su ogni altra superficie a contatto con il liquido"
Data una superficie fissata, se la forza aumenta la pressione aumenta.
Data una forza fissata, se la superficie aumenta la pressione diminuisce.
_
Tuttavia, alla pressione viene associata una forza di pressione, indicata con P , diretta come la normale alla superficie, quindi pressione e forza hanno stesso verso e direzione.
ps. Ai fini operativi in Pascal non è una unità di misura molto utile e le si preferisce un suo multiplo il Bar: 1 Bar = 10000 Pa
Sono molte però le unità di misura che persistono nell'uso comune in vari campi della scienza
In meteorologia l'unità più usata è un sottomultiplo del Bar, il milliBar
1 mBar = 1 Bar/ 1000
In medicina la pressione sanguigna e quella dei fluidi in generale viene ancora misurata in milimmetri di mercurio (mmHg). Cioè si misura la pressione, del sangue ad esempio, confrontandola con quella che esercita una colonnina di mercurio, anche se i moderni apparecchi per misurare la pressione sono ormai elettronici, ben diversi dai vecchi sfigmomanometri.
1 mmHg = 133.322 Pa
In chimica si usa ancora fare gli esercizi considerando le atmosfere. L'atmosfera (Atm) è una grandezza correlata direttamente alla pressione che esercita l'involucro gassoso terrestre sulla terra. Una unità di misura storicamente ricavata durante i primi esperimenti sui gas perfetti.
1 Atm = 760 mmHg = 101325 Pa
venerdì 29 marzo 2013
Una proprietà fisica dei corpi: la densità
Come detto nel post precedente "l'equilibrio dei fluidi" in questo post ci occuperemo della grandezza che è associata alla massa di un volume dato di un fluido, o in generale di un corpo.
Definiamo densità assoluta di un corpo la massa dell'unità di volume del corpo stesso e la indichiamo con il simbolo r (ro).
La densità assoluta o densità si ottiene tramite il rapporto tra la massa di un corpo e il suo volume
r = m/V(kg/m3)
dove r (ro) indica la densità o massa volumica;
m la massa del corpo; Esperienza di laboratorio: la densità
V il suo volume.
I materiali hanno densità differenti ecco perchè alcuni oggetti se messi in un recipiente pieno di acqua alcuni galleggiano altri affondano.
Possiamo notare che alcuni oggetti con volume identico hanno masse diverse e quindi affermare che la densità è una caratteristica del materiale di cui è fatto un oggetto.
Ricordiamo inoltre che le considerazione qui sopra dette sono avente caratteristiche con temperatura e pressione ambiente.
Concludendo l'acqua è una sostanza particolare per la determinazione della massa volumica, in quanto è la sostanza campione o di riferimento: la densità assoluta dell'acqua è 1 grammo al centimetro cubo alla temperatura di 4°C, nel S.I. è 1000 kg/m3.
Altro concetto che possiamo ora introdurre è la densità relativa che è il rapporto tra la densità assoluta dell'oggetto e la densità di una sostanza di riferimento che normalmente è l'acqua distillata a 4°C.
r rel= r / r H2O
Di seguito alcuni valori di densità di solidi, liquidi ed aeriforme, se vi interessano altri oggetti vi rimando a questo indirizzo: tabella completa
Definiamo densità assoluta di un corpo la massa dell'unità di volume del corpo stesso e la indichiamo con il simbolo r (ro).
La densità assoluta o densità si ottiene tramite il rapporto tra la massa di un corpo e il suo volume
r = m/V(kg/m3)
dove r (ro) indica la densità o massa volumica;
m la massa del corpo; Esperienza di laboratorio: la densità
V il suo volume.
I materiali hanno densità differenti ecco perchè alcuni oggetti se messi in un recipiente pieno di acqua alcuni galleggiano altri affondano.
Possiamo notare che alcuni oggetti con volume identico hanno masse diverse e quindi affermare che la densità è una caratteristica del materiale di cui è fatto un oggetto.
Ricordiamo inoltre che le considerazione qui sopra dette sono avente caratteristiche con temperatura e pressione ambiente.
Concludendo l'acqua è una sostanza particolare per la determinazione della massa volumica, in quanto è la sostanza campione o di riferimento: la densità assoluta dell'acqua è 1 grammo al centimetro cubo alla temperatura di 4°C, nel S.I. è 1000 kg/m3.
Altro concetto che possiamo ora introdurre è la densità relativa che è il rapporto tra la densità assoluta dell'oggetto e la densità di una sostanza di riferimento che normalmente è l'acqua distillata a 4°C.
r rel= r / r H2O
Di seguito alcuni valori di densità di solidi, liquidi ed aeriforme, se vi interessano altri oggetti vi rimando a questo indirizzo: tabella completa
| Nome
| Densità (g/cm³)
|
|---|---|
| Alluminio
| 2.70
|
| Argento
| 10.49
|
| Cemento
| 2.7-3.0
|
| Ferro
| 7.96
|
| Ghiaccio
| 0.92
|
| Legno (densità media)
| 0.75
|
| Legno di cedro
| 0.31-0.49
|
| Legno d'ebano
| 0.98
|
| Legno d'olmo
| 0.54-0.60
|
| Legno di pino bianco
| 0.35-0.50
|
| Legno di quercia
| 0.6-0.9
|
| Nichel
| 8.8
|
| Oro
| 19.3
|
| Ottone
| 8.44-9.70
|
| Osso
| 1.7-2.0
|
| Piombo
| 11.3
|
| Platino
| 21.37
|
| Rame
| 8.96
|
| Sughero
| 0.22-0.26
|
| Terra (valor medio*)
| 5.52
|
| Tungsteno
| 19.3
|
| Vetro
| 2.4-2.8
|
| Zinco
| 6.9 |
* Densità media della Terra (intesa come globo terrestre),
calcolata in base alla legge di attrazione newtoniana.[Enciclopedia Treccani,
vol.III, p.830, Ist.Poligrafico dello Stato, Roma, 1970].
| Nome
| Densità (g/cm³)
|
|---|---|
| Acqua
| 1.00
|
| Acqua di mare
| 1.025
|
| Alcool (etilico)
| 0.806
|
| Benzina
| 0.68
|
| Glicerina
| 1.261
|
| Mercurio
| 13.6
|
| Olio d'oliva
| 0.92
|
| Olio di paraffina
| 0.8 |
| Nome
| Formula
| Densità (g/dm³)
|
|---|---|---|
| Acetilene
| C2H2
| 1.173
|
| Aria
| 1.292
| |
| Ammoniaca
| NH3
| 0.771
|
| Diossido di carbonio
| CO2
| 1.976
|
| Monossido di carbonio
| CO
| 1.250
|
| Elio
| He
| 0.178
|
| Idrogeno
| H2
| 0.089
|
| Ossigeno
| O2
| 1.429
|
| Ozono
| O3
| 2.144 |
giovedì 28 marzo 2013
L'equilibrio dei fluidi
Consideriamo quei corpi che non hanno una forma propria, cioè corpi allo stato liquido e gassoso: corpi fluidi. Per studiare l'equilibrio statico dei fluidi ci costruiremo un modello "dei fluidi".
Parliamo di statica dei liquidi, meglio nota di Idrostatica.
Il modello di fluido viene applicato su liquidi qualsiasi, nel nostro caso studieremo l'acqua.
Trascurando il modello corpuscolare della materia e quindi tutte le sue particelle che la compongono che in tal caso andrebbero analizzate ogni singola molecole (impraticabile) per spiegarne l'equilibrio, dovute alle forze agenti intervenute sull'acqua, possiamo definire relativamente al problema dell'idrostatica un corpo (l'acqua) costituito da strati sovrapposti: le particelle di ogni strato sono sostanzialmente corpo rigidi, lastre rigide, che tuttavia possono scorrere gli uni sugli altri, trascurando l'attrito radente. In questi termini possiamo dire che tale movimento rappresenta un fluido ideale.
Il fluido ideale esclude la viscosità propria dei lquidi, tutti i movimenti di tipo vorticoso.
Dunque possiamo trasferire questo modello ai fluidi reali? Sicuramente quando parliamo del problema dell'equilibrio, vale a dire le condizioni che garantiscono che il corpo fluido resti fermo.
In idrostatica consideriamo un liquido nel suo insieme, ovvero dal suo punto di vista macroscopico, privo di attrito, nessun movimento vorticoso e viscosità nulla, un modello a strati sovrapposti.
Nel modello a strati sovrapposti, gli strati devono avere tutti lo stesso volume DV.
Si può concludere che suddividendo il fluido in strati induce a ricercare una relazione, tra massa e volume di un corpo che sia esprimibile mediante una grandezza fisica ma di questo ne parleremo nel prossimo post.
Parliamo di statica dei liquidi, meglio nota di Idrostatica.
Il modello di fluido viene applicato su liquidi qualsiasi, nel nostro caso studieremo l'acqua.
Trascurando il modello corpuscolare della materia e quindi tutte le sue particelle che la compongono che in tal caso andrebbero analizzate ogni singola molecole (impraticabile) per spiegarne l'equilibrio, dovute alle forze agenti intervenute sull'acqua, possiamo definire relativamente al problema dell'idrostatica un corpo (l'acqua) costituito da strati sovrapposti: le particelle di ogni strato sono sostanzialmente corpo rigidi, lastre rigide, che tuttavia possono scorrere gli uni sugli altri, trascurando l'attrito radente. In questi termini possiamo dire che tale movimento rappresenta un fluido ideale.
Il fluido ideale esclude la viscosità propria dei lquidi, tutti i movimenti di tipo vorticoso.
Dunque possiamo trasferire questo modello ai fluidi reali? Sicuramente quando parliamo del problema dell'equilibrio, vale a dire le condizioni che garantiscono che il corpo fluido resti fermo.
In idrostatica consideriamo un liquido nel suo insieme, ovvero dal suo punto di vista macroscopico, privo di attrito, nessun movimento vorticoso e viscosità nulla, un modello a strati sovrapposti.
Nel modello a strati sovrapposti, gli strati devono avere tutti lo stesso volume DV.
Si può concludere che suddividendo il fluido in strati induce a ricercare una relazione, tra massa e volume di un corpo che sia esprimibile mediante una grandezza fisica ma di questo ne parleremo nel prossimo post.
Solido, liquido, gas(aeriforme)
Prima di descrivere e soffermarci su liquidi e gas, facciamo un punto sulle differenze tra un corpo solido, liquido ed aeriforme.
Il solido può essere afferrato e spostato come se fosse un oggetto unico.
Il solido è un corpo rigido e come tale conserva forma e volume. Ricordo che per corpi rigidi vengono definiti quei corpi che dotati di dimensione, mantengono la loro forma pur sottoposti a forze esterne (deformazioni apprezzabili).
Il liquido è un fluido che assume la forma del recipiente che lo contiene. Ha un volume proprio: è difficile comprimerlo in un volume più piccolo. Ovvio dire che i liquidi non hanno forma propria tanto più i fluidi.
Per i gas ( o aeriforme) a differenza dei corpi solidi e liquidi, non si può parlare di volume proprio. occupa tutto il suol volume del recipiente che lo contiene. Può essere compresso in un volume più piccolo.Una quantità d'aria racchiusa in cilindro con uno stantuffo a tenuta stagna occupa tutto il volume a disposizione, ma se lo stantuffo viene sollevato o abbassato, il volume interno del cilindro aumenta o diminuisce e l'aria occupa completamente il nuovo volume, diradandosi o comprimendosi.
Se ragioniamo a temperatura ambiente (20°C) abbiamo sostanze solide: ferro, sale da cucina , rame, alluminio, ecc.
Liquide: benzina, olio d'oliva, mercurio.
Gassosi: l'ossigeno, il metano, l'azoto, il propano, il butano, ecc.
Concludiamo dicendo che le sostanze possono cambiare forma a seconda delle condizioni (temperatura e pressione) in cui si trovano, pensiamo all'acqua, può essere solido, liquido e gassosa e pertanto non è una proprietà assoluta.
Il solido può essere afferrato e spostato come se fosse un oggetto unico.
Il solido è un corpo rigido e come tale conserva forma e volume. Ricordo che per corpi rigidi vengono definiti quei corpi che dotati di dimensione, mantengono la loro forma pur sottoposti a forze esterne (deformazioni apprezzabili).
Il liquido è un fluido che assume la forma del recipiente che lo contiene. Ha un volume proprio: è difficile comprimerlo in un volume più piccolo. Ovvio dire che i liquidi non hanno forma propria tanto più i fluidi.
Per i gas ( o aeriforme) a differenza dei corpi solidi e liquidi, non si può parlare di volume proprio. occupa tutto il suol volume del recipiente che lo contiene. Può essere compresso in un volume più piccolo.Una quantità d'aria racchiusa in cilindro con uno stantuffo a tenuta stagna occupa tutto il volume a disposizione, ma se lo stantuffo viene sollevato o abbassato, il volume interno del cilindro aumenta o diminuisce e l'aria occupa completamente il nuovo volume, diradandosi o comprimendosi.
Se ragioniamo a temperatura ambiente (20°C) abbiamo sostanze solide: ferro, sale da cucina , rame, alluminio, ecc.
Liquide: benzina, olio d'oliva, mercurio.
Gassosi: l'ossigeno, il metano, l'azoto, il propano, il butano, ecc.
Concludiamo dicendo che le sostanze possono cambiare forma a seconda delle condizioni (temperatura e pressione) in cui si trovano, pensiamo all'acqua, può essere solido, liquido e gassosa e pertanto non è una proprietà assoluta.
martedì 26 marzo 2013
La legge di Hooke
Un materiale ha un comportamento elastico quando, al cessare della sollecitazione meccanica che lo ha deformato, ritorna nel suo stato iniziale, senza conservare in sè nessuna alterazione dipendente dalla forza che gli è stata applicata.
Possiamo formulare la legge di elasticità dei corpi come segue: l'allungamento di una molla è direttamente proporzionale alla forza esterna che lo ha prodotto.
Il legame matematico è il seguente: F=K DL
dove DL= lf - li; ( l'allungamento finale meno l'allungamento iniziale)
K è la costante di di proporzionalità, detta costante eleastica, è una caratteristica della molla, che dipende dalla materiale e dalle caratteristiche costruttive (numero di spire, diametro delle spire, ecc.)
La legge di Hooke è valida solo per piccole deformazioni o per valori non elevati, almeno fin quando subìto la deformazione, la molla, ritorna al suo stato iniziale, altresì si rischia la rottura perdendo l'elasticità della molla iniziale ed ottenendo una deformazione permanente.
esperienza di laboratorio: la legge di Hooke
Possiamo formulare la legge di elasticità dei corpi come segue: l'allungamento di una molla è direttamente proporzionale alla forza esterna che lo ha prodotto.
Il legame matematico è il seguente: F=K DL
dove DL= lf - li; ( l'allungamento finale meno l'allungamento iniziale)
K è la costante di di proporzionalità, detta costante eleastica, è una caratteristica della molla, che dipende dalla materiale e dalle caratteristiche costruttive (numero di spire, diametro delle spire, ecc.)
La legge di Hooke è valida solo per piccole deformazioni o per valori non elevati, almeno fin quando subìto la deformazione, la molla, ritorna al suo stato iniziale, altresì si rischia la rottura perdendo l'elasticità della molla iniziale ed ottenendo una deformazione permanente.
esperienza di laboratorio: la legge di Hooke
mercoledì 20 marzo 2013
Il piano inclinato
Il piano inclinato è una macchina semplice che ci permette di risparmiare forza per sollevare un corpo ad una quota h.
Definizione "Lo sforzo di trazione o di spinta impiegato per muovere verso l'alto di un corpo pesante lungo un piano inlinato di lunghezza L è altezza h è pari al prodotto del peso del corpo P per il rapporto h/L (pendenza del piano)".
La legge dunque si traduce nella seguente equazione Fe=P.(h/L).
La relazione che lega la forza equilibrante Fe e la relativa altezza h è una proporzionalità diretta.
esperienza di laboratorio: il piano inclinato vai all' esperienze di laboratorio
Definizione "Lo sforzo di trazione o di spinta impiegato per muovere verso l'alto di un corpo pesante lungo un piano inlinato di lunghezza L è altezza h è pari al prodotto del peso del corpo P per il rapporto h/L (pendenza del piano)".
La legge dunque si traduce nella seguente equazione Fe=P.(h/L).
La relazione che lega la forza equilibrante Fe e la relativa altezza h è una proporzionalità diretta.
esperienza di laboratorio: il piano inclinato vai all' esperienze di laboratorio
lunedì 18 marzo 2013
Le leve
Applichiamo le condizioni di equilibrio di un corpo rigido alle leve, che sono dispositivi per aumentare o ridurre le forze.
Una leve è costituita da un corpo rigido libero di ruotare attorno al punto O, detto Fulcro, sotto l'azione di una forza F, detta forza agente o potenza, e di una forza R, detta forza resistente o resistenza , applicate in punti a distanza bp braccio della potenza, e a distanza br braccio della resistenza, dal punto O.
La leva per essere in equilibrio, ricordiamo che devono essere rispettata la condizione in cui la somma dei momenti sia uguale a zero ovvero Mf – Mr = 0 cioè F. bf = R. br
Una leve è costituita da un corpo rigido libero di ruotare attorno al punto O, detto Fulcro, sotto l'azione di una forza F, detta forza agente o potenza, e di una forza R, detta forza resistente o resistenza , applicate in punti a distanza bp braccio della potenza, e a distanza br braccio della resistenza, dal punto O.
La leva per essere in equilibrio, ricordiamo che devono essere rispettata la condizione in cui la somma dei momenti sia uguale a zero ovvero Mf – Mr = 0 cioè F. bf = R. br
da questa relazione si deduce
che la leva è in equilibrio quando la
potenza e la resistenza sono inversamente proporzionali ai rispettivi bracci.
esperienza di laboratorio: le leve vai all'esperienza di laboratorio
domenica 17 marzo 2013
Equilibrio di un corpo rigido soggetto al proprio peso (baricentro)
Abbiamo detto che le forze affinchè siano in equilibrio hanno un forza agente dall'esterno e una forza reazione vincolare che si oppone alla prima.
Mentre sappiamo che una sedia su un pavimento ha la reazione vincolare del pavimento, non sappiamo invece dov'è applicata la forza pesa della sedia, quindi si introduce un nuovo concetto:il baricentro!
definizione di baricentro: " il punto in cui si può pensare sia concentrato tutto il peso del corpo".
Considerando corpi omogenei (stesso materiale) e di spessore costante, la posizione del baricentro coincide con il centro geometrico della figura piana che rappresenta il corpo.
esempio: in un quadrato disegnato su un foglio tracciando le diagonale otteniamo un punto al centro ovvero il baricentro.
Possiamo concludere dicendo che ci sono tre tipi di equilibrio:
equilibrio stabile = il baricentro è più basso del punto di applicazione del vincolo;
equilibrio instabile= il baricentro e il vincolo stanno sulla stessa verticale con il baricentro più in alto del vincolo.
equilibrio indifferente= il baricentro e il vincolo coincidono.
Esperienza di laboratorio: il baricentro sperimentale
Mentre sappiamo che una sedia su un pavimento ha la reazione vincolare del pavimento, non sappiamo invece dov'è applicata la forza pesa della sedia, quindi si introduce un nuovo concetto:il baricentro!
definizione di baricentro: " il punto in cui si può pensare sia concentrato tutto il peso del corpo".
Considerando corpi omogenei (stesso materiale) e di spessore costante, la posizione del baricentro coincide con il centro geometrico della figura piana che rappresenta il corpo.
esempio: in un quadrato disegnato su un foglio tracciando le diagonale otteniamo un punto al centro ovvero il baricentro.
Possiamo concludere dicendo che ci sono tre tipi di equilibrio:
equilibrio stabile = il baricentro è più basso del punto di applicazione del vincolo;
equilibrio instabile= il baricentro e il vincolo stanno sulla stessa verticale con il baricentro più in alto del vincolo.
equilibrio indifferente= il baricentro e il vincolo coincidono.
Esperienza di laboratorio: il baricentro sperimentale
Condizioni di equilibrio per un corpo rigido esteso
Un corpo rigido esteso, sotto l'azione di un sistema di forze, può compiere due diversi tipi di movimento:
- un moto rotatorio sotto l'azione di un sistema di forze equivalente a un momento, in cui i punti del corpo compiono spostamenti diversi attorno al centro di rotazione: per esempio una giostra ruota attorno al suo asse sotto l'azione del momento provocato dalla coppia motrice;
- un moto traslatorio sotto l'azione di un sistema di forze equivalente a una sola forza, la risultante, in cui tutti i punti del corpo compiono lo stesso spostamento: per esempio il treno trasla lungo le rotaie sotto l'azione della forza motrice.
Ora la domanda da chiedersi è quali forze agiscono su un corpo rigido? facciamo un esempio: un uomo è in piedi sul pavimento, le forze che costituiscono il sistema sono la forza del nostro peso (forza verticale) diretta verso il basso e la forza del pavimento che si oppone alla forza esercitata dall'uomo dal basso verso l'alto, possiamo quindi dare un nome alle forze: la prima forza attiva, la seconda reazione vincolare.
definizione " la reazione vincolare è quindi una forza che si oppone al movimento per effetto di una causa esterna che limita le possibilità di spostamento di un corpo"
quindi la reazione vincolare è l'equilibrante delle forze esterne.
per garantire l'equilibrio alla traslazione di un corpo deve far si che la forza agente e la reazione vincolare siano uguale a zero: S Fi = 0 che si legge sommatoria di tutte le forze uguale a zero.
Stesso discorso possiamo farlo per il moto rotatorio.. affinchè si ci sia equilibrio il sistema di tutti i momenti sia uguale a zero: S Mi = 0
prova di laboratorio: equilibrio dei momenti vai all' esperienze di laboratorio
- un moto rotatorio sotto l'azione di un sistema di forze equivalente a un momento, in cui i punti del corpo compiono spostamenti diversi attorno al centro di rotazione: per esempio una giostra ruota attorno al suo asse sotto l'azione del momento provocato dalla coppia motrice;
- un moto traslatorio sotto l'azione di un sistema di forze equivalente a una sola forza, la risultante, in cui tutti i punti del corpo compiono lo stesso spostamento: per esempio il treno trasla lungo le rotaie sotto l'azione della forza motrice.
Ora la domanda da chiedersi è quali forze agiscono su un corpo rigido? facciamo un esempio: un uomo è in piedi sul pavimento, le forze che costituiscono il sistema sono la forza del nostro peso (forza verticale) diretta verso il basso e la forza del pavimento che si oppone alla forza esercitata dall'uomo dal basso verso l'alto, possiamo quindi dare un nome alle forze: la prima forza attiva, la seconda reazione vincolare.
definizione " la reazione vincolare è quindi una forza che si oppone al movimento per effetto di una causa esterna che limita le possibilità di spostamento di un corpo"
quindi la reazione vincolare è l'equilibrante delle forze esterne.
per garantire l'equilibrio alla traslazione di un corpo deve far si che la forza agente e la reazione vincolare siano uguale a zero: S Fi = 0 che si legge sommatoria di tutte le forze uguale a zero.
Stesso discorso possiamo farlo per il moto rotatorio.. affinchè si ci sia equilibrio il sistema di tutti i momenti sia uguale a zero: S Mi = 0
prova di laboratorio: equilibrio dei momenti vai all' esperienze di laboratorio
giovedì 7 marzo 2013
Cambiamento di stato
Il cambiamento di stato non è altro che "un passaggio da uno stato di aggregazione molecolare ad un altro".
Le proprietà dei cambiamenti di stato sono:
1) Per ogni sostanza, dipendono dalla temperatura T, che rimane costante;
2) Dipendono dalla pressione p (più bassa e p, più bassa è "T");
3) Sono reversibili, cioè possono avvenire sia nella direzione solido-liquido-gasssoso che nella direzione opposta gassoso-liquido-solido, con temperatura di fusione=temperatura di solidificazione, temperatura di vaporizzazione=temporizzazione di condensazione, temperatura di sublimazione=temperatura di sublimazione.
4) Nella reversibilità ovvero nella direzione solido-liquido-gassoso c'è un assorbimento di calore, nella direzione gassoso-liquido-solido c'è una perdita di calore.
La quantità di calore variata (assorbita e perduta) in una trasformazione di stato non dipende dalla temperatura, dipende da:
a) Pressione (soprattutto la vaporizzazione e condensazione);
b) Massa della sostanza;
c) Il tipo di sostanza, caratterizzata dal calore latente (latente cioè nascosto, poichè non varia la temperatura).
Variazione di calore= calore latente * massa
DQ=K*m
Fusione, Condensazione
DQF=KF*m
Ebollizione (a pressione fissata) Condensazione
DQeb=Keb*m
Il calore latente K= DQ/m (cal/gr.) è il calore necessario per trasformare l'unità di massa di una sostanza da una fase all'altra.
Nota1
EBOLLIZIONE= processo forzato, rapido, che coinvolge tutta la massa fluida;
avviene quando "pressione esterna"= pressione interna di 2 fasi compresenti
(liquido + vapore).
EVAPORIZZAZIONE: dipende da temperatura (più alta T, più evapora);
dipende da pressione (più alta p, meno evapora);
è un fenomeno superficiale.
Nota2
Gli scambi di calore che producono dilatazione termica implicano una variazione di temperatura e sono regolati dalla relazione DQ= c*m*D t
Gli scambi di calore che producono variazione di stato si svolgono a temperatura costante e sono regolati dalla relazione DQ=K*m
Vedi scheda di laboratorio diagramma e schema a blocchi
Per altre schedi di laboratorio vedi esperienze di laboratorio
Le proprietà dei cambiamenti di stato sono:
1) Per ogni sostanza, dipendono dalla temperatura T, che rimane costante;
2) Dipendono dalla pressione p (più bassa e p, più bassa è "T");
3) Sono reversibili, cioè possono avvenire sia nella direzione solido-liquido-gasssoso che nella direzione opposta gassoso-liquido-solido, con temperatura di fusione=temperatura di solidificazione, temperatura di vaporizzazione=temporizzazione di condensazione, temperatura di sublimazione=temperatura di sublimazione.
4) Nella reversibilità ovvero nella direzione solido-liquido-gassoso c'è un assorbimento di calore, nella direzione gassoso-liquido-solido c'è una perdita di calore.
La quantità di calore variata (assorbita e perduta) in una trasformazione di stato non dipende dalla temperatura, dipende da:
a) Pressione (soprattutto la vaporizzazione e condensazione);
b) Massa della sostanza;
c) Il tipo di sostanza, caratterizzata dal calore latente (latente cioè nascosto, poichè non varia la temperatura).
Variazione di calore= calore latente * massa
DQ=K*m
Fusione, Condensazione
DQF=KF*m
Ebollizione (a pressione fissata) Condensazione
DQeb=Keb*m
Il calore latente K= DQ/m (cal/gr.) è il calore necessario per trasformare l'unità di massa di una sostanza da una fase all'altra.
Nota1
EBOLLIZIONE= processo forzato, rapido, che coinvolge tutta la massa fluida;
avviene quando "pressione esterna"= pressione interna di 2 fasi compresenti
(liquido + vapore).
EVAPORIZZAZIONE: dipende da temperatura (più alta T, più evapora);
dipende da pressione (più alta p, meno evapora);
è un fenomeno superficiale.
Nota2
Gli scambi di calore che producono dilatazione termica implicano una variazione di temperatura e sono regolati dalla relazione DQ= c*m*D t
Gli scambi di calore che producono variazione di stato si svolgono a temperatura costante e sono regolati dalla relazione DQ=K*m
Vedi scheda di laboratorio diagramma e schema a blocchi
Per altre schedi di laboratorio vedi esperienze di laboratorio
giovedì 21 febbraio 2013
Il momento delle forze
Un corpo rigido, a differenza del punto materiale, può anche ruotare.
"Il braccio di una forza F rispetto a un punto O è dato dalla distanza tra il punto O e la retta che contiene F"
Definiamo quindi il momento di una forza come "Il movimento di una forza F rispetto a un punto O è uguale al prodotto dell'intensità F della forza per il braccio b".
M=F b F=M/b b=M/F (ricorda b=braccio)
Il momento della forza ha segno positivo se ruota in senso antiorario, negativo in senso orario.
L'unità di misura del momento è N m.
Il momento di una coppia di forze è data da due forze, uguali e opposte, applicate in due punti diversi di un corpo rigido.
"Definiamo il momento di una coppia come la somma dei momenti delle forze rispetto al punto mediio O. Esso è uguale al prodotto dell'intensità F di una forza per la distanza d tra le rette di azione delle due forze"
M= F d
esempio: pensiamo alla chiave nella toppa della serratura, ad una bici quando ruotiamo il manubrio, la maniglia di una porta, ecc
quindi M=Fb + Fb dove d= distanza e comprende i due bracci b1+b2
i segni sono come per il momento della forza visto sopra antiorario=positivo e orario=negativo
Il momento di una forza è una grandezza vettoriale avente la drezione perpendicolare al piano individuato da r e F e verso offerto dalla regola della mano destra allorquando r si sovrappone ad F descrivendo l'angolo alfa
possiamo scrivere cosi il prodotto verttoriale: M = r∧ F
ed in modulo: M = r F senϑ dove senϑ è l'angolo che si forma tra due vettori; ed M è dato dalla regola della mano destra.
"Il braccio di una forza F rispetto a un punto O è dato dalla distanza tra il punto O e la retta che contiene F"
Definiamo quindi il momento di una forza come "Il movimento di una forza F rispetto a un punto O è uguale al prodotto dell'intensità F della forza per il braccio b".
M=F b F=M/b b=M/F (ricorda b=braccio)
Il momento della forza ha segno positivo se ruota in senso antiorario, negativo in senso orario.
L'unità di misura del momento è N m.
Il momento di una coppia di forze è data da due forze, uguali e opposte, applicate in due punti diversi di un corpo rigido.
"Definiamo il momento di una coppia come la somma dei momenti delle forze rispetto al punto mediio O. Esso è uguale al prodotto dell'intensità F di una forza per la distanza d tra le rette di azione delle due forze"
M= F d
esempio: pensiamo alla chiave nella toppa della serratura, ad una bici quando ruotiamo il manubrio, la maniglia di una porta, ecc
quindi M=Fb + Fb dove d= distanza e comprende i due bracci b1+b2
i segni sono come per il momento della forza visto sopra antiorario=positivo e orario=negativo
Il momento di una forza è una grandezza vettoriale avente la drezione perpendicolare al piano individuato da r e F e verso offerto dalla regola della mano destra allorquando r si sovrappone ad F descrivendo l'angolo alfa
possiamo scrivere cosi il prodotto verttoriale: M = r∧ F
ed in modulo: M = r F senϑ dove senϑ è l'angolo che si forma tra due vettori; ed M è dato dalla regola della mano destra.
domenica 17 febbraio 2013
Effetto di più forze su un corpo rigido
Due o più forze applicate ad un punto materiale danno una forza risultante che è la somma delle forze applicate. Tutto questo è vero fino ad un certo punto, infatti constatato che
"una forza che agisce su un corpo rigido può essere spostata lungo la sua retta d'azione in un altro punto dello stesso corpo, senza che l'effetto della forza cambi".
Possono verificarsi casi diversi tipo:
1) le forze sono applicate lungo la stessa retta d'azione;
2) le forze sono dette parallele (concordi e discordi);
3) le forze agiscono lungo rette d'azione che s'intersecano, in questo caso si dicono concorrenti.
caso 1 stessa retta d'azione
caso 2 parallele discordi
caso 3 concorrenti (si applica la regola del parallelogramma)
"una forza che agisce su un corpo rigido può essere spostata lungo la sua retta d'azione in un altro punto dello stesso corpo, senza che l'effetto della forza cambi".
Possono verificarsi casi diversi tipo:
1) le forze sono applicate lungo la stessa retta d'azione;
2) le forze sono dette parallele (concordi e discordi);
3) le forze agiscono lungo rette d'azione che s'intersecano, in questo caso si dicono concorrenti.
caso 1 stessa retta d'azione
caso 2 parallele concordi caso 2 parallele discordi
caso 3 concorrenti (si applica la regola del parallelogramma)
venerdì 15 febbraio 2013
Laboratorio:misure con il calibro e il righello
Una prova che non manca mai nel programma di laboratorio di fisica è la misura diretta con uno strumento di misura molto usato non solo in laboratorio ma anche nella vita quotidiana, a casa, sul lavoro, nell'officine ecc. Stiamo parlando del calibro a cursore, uno strumento molto preciso ed accurato.
Per la descrizione del calibro e del modello della prova di laboratorio vi rimando ai seguenti link:
istruzioni uso calibro misura di un oggetto con il calibro
ps. le immagini de istruzioni uso calibro non si vedono bene pertanto vi rimando al seguente link:
uso del calibro ricerca sul calibro istruzioni
Per la descrizione del calibro e del modello della prova di laboratorio vi rimando ai seguenti link:
istruzioni uso calibro misura di un oggetto con il calibro
ps. le immagini de istruzioni uso calibro non si vedono bene pertanto vi rimando al seguente link:
uso del calibro ricerca sul calibro istruzioni
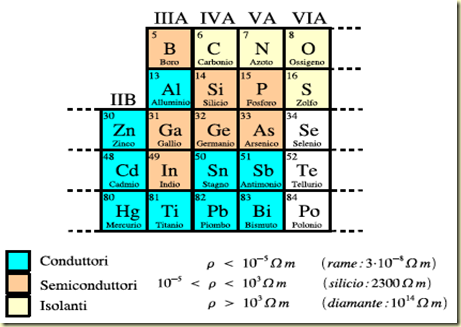
Conduttori, semiconduttori e isolanti
Le sostanze che favoriscono al loro interno il passaggio della corrente elettrica sono dette conduttori; quelle invece che impediscono il passaggio della corrente sono dette isolanti.
Solo poche sostanze, principalmente i metalli, sono buoni conduttori dell’elettricità. Ciò dipende dal fatto che i metalli sono composti da atomi che hanno una struttura elettronica costituita da una serie di livelli (bande) completamente occupati ed un livello più esterno non completamente occupato, contenente uno, due o a volte anche tre elettroni di valenza . Nei metalli allo stato solido, gli elettroni di valenza sono praticamente liberi di muoversi; essi si trovano in un livello di energia più elevato: si dice che sono in banda di conduzione.
Un campo elettrico applicato al metallo, anche se piccolo, produce un moto di deriva e quindi una corrente elettrica.
In molte sostanze tuttavia, gli elettroni di valenza sono legati agli ioni positivi del reticolo. A causa della mancanza di elettroni liberi e quindi di portatori di carica, in queste sostanze è molto difficile produrre una corrente elettrica ; queste sostanze sono chiamate dielettrici e sono isolanti.
Vi è un’altra categoria di sostanze, chiamate semiconduttori costituite da materiali che hanno un comportamento diverso sia dai conduttori che dagli isolanti. In essi gli elettroni riempiono tutta la banda di valenza e non vi sono elettroni “liberi” nella banda di conduzione, proprio come negli isolanti. Nei semiconduttori, però, l’energia necessaria per far passare un elettrone dalla banda di valenza a quella di conduzione è circa da 1/5 a 1/10 dell’energia di eccitazione di un isolante.
Un aumento di temperatura può avere l’effetto di liberare alcuni elettroni dai loro legami e mandarli in banda di conduzione. I semiconduttori hanno quindi una conducibilità elettrica.
I semiconduttori più usati sono germanio, silicio, tellurio.
Solo poche sostanze, principalmente i metalli, sono buoni conduttori dell’elettricità. Ciò dipende dal fatto che i metalli sono composti da atomi che hanno una struttura elettronica costituita da una serie di livelli (bande) completamente occupati ed un livello più esterno non completamente occupato, contenente uno, due o a volte anche tre elettroni di valenza . Nei metalli allo stato solido, gli elettroni di valenza sono praticamente liberi di muoversi; essi si trovano in un livello di energia più elevato: si dice che sono in banda di conduzione.
Un campo elettrico applicato al metallo, anche se piccolo, produce un moto di deriva e quindi una corrente elettrica.
In molte sostanze tuttavia, gli elettroni di valenza sono legati agli ioni positivi del reticolo. A causa della mancanza di elettroni liberi e quindi di portatori di carica, in queste sostanze è molto difficile produrre una corrente elettrica ; queste sostanze sono chiamate dielettrici e sono isolanti.
Vi è un’altra categoria di sostanze, chiamate semiconduttori costituite da materiali che hanno un comportamento diverso sia dai conduttori che dagli isolanti. In essi gli elettroni riempiono tutta la banda di valenza e non vi sono elettroni “liberi” nella banda di conduzione, proprio come negli isolanti. Nei semiconduttori, però, l’energia necessaria per far passare un elettrone dalla banda di valenza a quella di conduzione è circa da 1/5 a 1/10 dell’energia di eccitazione di un isolante.
Un aumento di temperatura può avere l’effetto di liberare alcuni elettroni dai loro legami e mandarli in banda di conduzione. I semiconduttori hanno quindi una conducibilità elettrica.
I semiconduttori più usati sono germanio, silicio, tellurio.
tabella materiali conduttori
Il coefficiente di temperatura a0 viene fornito per una temperatura di riferimento di 0 °C. Qualora si abbia una temperatura di riferimento f °C, il nuovo valore di af si ricava dalla formula:
af = a0 / 1 + a0 x f
Tabella semiconduttori
| |||||||||
Multipli e sottomultipli, unità fondamentali e derivate
Unità fondamentali
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Grandezza fisica
|
Simbolo della
grandezza
|
Nome dell'unità SI
|
Simbolo dell'unità SI
|
|---|---|---|---|
l
|
m
| ||
m
|
kg
| ||
t
|
s
| ||
I, i
|
A
| ||
T
|
K
| ||
n
|
mol
| ||
Iv
|
cd
|
Unità derivate
Grandezza fisica
|
Simbolo della
grandezza
|
Nome dell'unità SI
|
Simbolo dell'unità SI
|
Equivalenza in termini di unità fondamentali SI
| |
|---|---|---|---|---|---|
f, ν
|
Hz
|
s−1
| |||
F
|
N
|
kg · m · s−2
| |||
p
|
Pa
|
N · m−2
|
= kg · m−1 · s−2
| ||
E, Q
|
J
|
N · m
|
= kg · m2 · s−2
| ||
P, W
|
W
|
J · s−1
|
= kg · m2 · s−3
| ||
q
|
C
|
A · s
| |||
V, E
|
V
|
J · C−1
|
= m2 · kg · s−3 · A−1
| ||
R
|
Ω
|
V · A−1
|
= m2 · kg · s−3 · A−2
| ||
G
|
S
|
A · V−1
|
= s3 · A2 · m−2 · kg−1
| ||
C
|
F
|
C · V−1
|
= s4 · A2 · m−2 · kg−1
| ||
B
|
T
|
V · s · m−2
|
= kg · s−2 · A−1
| ||
Φ(B)
|
Wb
|
V · s
|
= m2 · kg · s−2 · A−1
| ||
L
|
H
|
V · s · A−1
|
= m2 · kg · s−2 · A−2
| ||
T
|
°C
|
K[2]
| |||
φ, θ
|
rad
|
1
|
= m · m−1
| ||
Ω
|
sr
|
1
|
= m2 · m−2
| ||
lm
|
cd · sr
| ||||
lx
|
cd · sr · m−2
| ||||
D
|
D
|
m−1
| |||
A
|
Bq
|
s−1
| |||
D
|
Gy
|
J · kg−1
|
= m2 · s−2
| ||
H
|
Sv
|
J · kg−1
|
= m2 · s−2
| ||
E
|
Sv
|
J · kg−1
|
= m2 · s−2
| ||
kat
|
mol · s−1
| ||||
A
|
m2
| ||||
V
|
m3
| ||||
v
|
m · s−1
| ||||
ω
|
s−1
rad · s−1
| ||||
a
|
m · s−2
| ||||
N · m
|
= m2 · kg · s−2
| ||||
n
|
m−1
| ||||
ρ
|
kg · m−3
| ||||
volume specifico
|
m3 · kg−1
| ||||
mol · dm−3
| |||||
Vm
|
m3 · mol−1
| ||||
C, S
|
J · K−1
|
= m2 · kg · s−2 · K−1
| |||
calore molare, entropia molare
|
Cm, Sm
|
J · K−1 · mol−1
|
= m2 · kg · s−2 · K−1 · mol−1
| ||
calore specifico, entropia specifica
|
c, s
|
J · K−1 · kg−1
|
= m2 · s−2 · K−1
| ||
energia molare
|
Em
|
J · mol−1
|
= m2 · kg · s−2 · mol−1
| ||
energia specifica
|
e
|
J · kg−1
|
= m2 · s−2
| ||
densità di energia
|
U
|
J · m−3
|
= m−1 · kg · s−2
| ||
σ
|
N · m−1
|
= J · m−2
= kg · s−2
| |||
densità di flusso calorico, irradianza
|
σ
|
W · m−2
|
= kg · s−3
| ||
W · m−1 · K−1
|
= m · kg · s−3 · K−1
| ||||
η
|
m2 · s−1
| ||||
ρ
|
N · s · m−2
|
= Pa · s
= m−1 · kg · s−1
| |||
densità di carica elettrica
|
C · m−3
|
= m−3 · s · A
| |||
densità di corrente elettrica
|
j
|
A · m−2
| |||
ρ
|
S · m−1
|
= m−3 · kg−1 · s3 · A2
| |||
conduttività molare
|
ρ
|
S · m2 · mol−1
|
= kg−1 · mol−1 · s3 · A2
| ||
ε
|
F · m−1
|
= m−3 · kg−1 · s4 · A2
| |||
μ
|
H · m−1
|
= m · kg · s−2 · A−2
| |||
(intensità) di campo elettrico
|
F, E
|
V · m−1
|
= m · kg · s−3 · A−1
| ||
(intensità) di campo magnetico
|
H
|
A · m−1
| |||
M
|
A · m−1
| ||||
cd · m−2
| |||||
esposizione (raggi X e gamma)
|
C · kg−1
|
= kg−1 · s · A
| |||
tasso di dose assorbita
|
Gy · s−1
|
= m2 · s−3
| |||
Iscriviti a:
Post (Atom)